webgl 世界 matrix 入门

In 未分类 on 2017年01月16日 by TAT.vorshen view: 7,212

这次没有带来游戏啦，本来还是打算用一个小游戏来介绍阴影，但是发现阴影这块想完完整整介绍一次太大了，涉及到很多，再加上业务时间的紧张，所以就暂时放弃了游戏，先好好介绍一遍 webgl 中的 Matrix。
这篇文章算是 webgl 的基础知识，因为如果想不走马观花的说阴影的话，需要打牢一定的基础，文章中我尽力把知识点讲的更易懂。内容偏向刚上手 webgl 的同学，至少知道着色器是什么，webgl 中 drawElements 这样的 API 会使用~

文章的标题是 Matrix is magic，矩阵对于 3D 世界来说确实是魔法一般的存在，说到 webgl 中的矩阵，PMatrix／VMatrix／MMatrix 这三个大家相信不会陌生，那就正文 let's go~

1/ 矩阵的来源
刚刚有说到 PMatrix／VMatrix／MMatrix 这三个词，他们中的 Matrix 就是矩阵的意思，矩阵是干什么的？用来改变顶点位置信息的，先牢记这句话，然后我们先从 canvas2D 入手相信一下我们有一个 100*100 的 canvas 画布，然后画一个矩形

ctx.rect(40, 40, 20, 20);

ctx.fill();

代码很简单，在画布中间画了一个矩形

现在我们希望将圆向左移动 10px

1 2	ctx.rect(30, 40, 20, 20); ctx.fill();

结果如下：

源码地址：https://vorshen.github.io/3Dmaze/1.html
结果展示：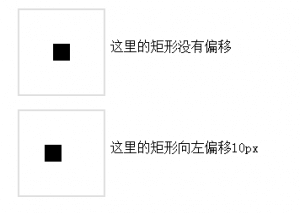

改变 rect 方法第一个参数就可以了，很简单，因为 rect() 对应的就是一个矩形，是一个对象，canvas2D 是对象级别的画布操作，而 webgl 不是，webgl 是片元级别的操作，我们操作的是顶点
用 webgl 如何画一个矩形？地址如下，可以直接查看源码

源码地址：https://vorshen.github.io/3Dmaze/2.html
结果展示：

这里我们可以看到 position 这个数组，这里面存的就是矩形 4 个点的顶点信息，我们可以通过操作改变其中点的值来改变位置 (页面源码也可以看到实现)，但是扪心自问这样不累吗？有没有可以一次性改变某个物体所有顶点的方式呢？
有，那就是矩阵，magic is coming

1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

上面这个是一个单位矩阵（矩阵最基础的知识这里就不说了），我们用这个乘一个顶点 (2,1,0) 来看看

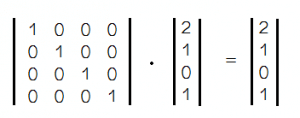
并没有什么变化啊！那我们换一个矩阵来看

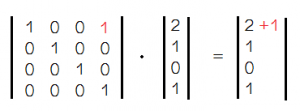
1 0 0 1
0 1 0 0
0 0 1 0
0 0 0 1

再乘之前那个顶点，发现顶点的 x 已经变化了！

如果你再多用几个顶点试一下就会发现，无论我们用哪个顶点，都会得到这样的一个 x 坐标+1 这样一个结果
来，回忆一下我们之前的目的，现在是不是有了一种一次性改变顶点位置的方式呢？

2/ 矩阵规律介绍
刚刚我们改变了矩阵 16 个值中的一个，就使得矩阵有改变顶点的能力，我们能否总结一下矩阵各个值的规律呢？当然是可以的，如下图

这里红色的 x，y，z 分别对应三个方向上的偏移

这里蓝色的 x，y，z 分别对应三个方向上的缩放

然后是经典的围绕各个轴的旋转矩阵 (记忆的时候注意围绕 y 轴旋转时，几个三角函数的符号……)

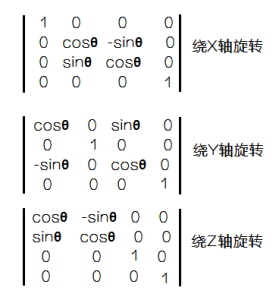
还有剪切 (skew) 效果的变换矩阵，这里用个 x 轴的例子来体现

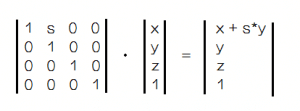
这里都是某一种单一效果的变化矩阵，可以相乘配合使用的，很简单。我们这里重点来找一下规律，似乎所有的操作都是围绕着红框这一块来的

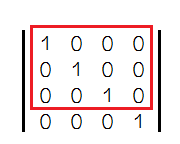
其实也比较好理解，因为矩阵这里每一行对应了个坐标

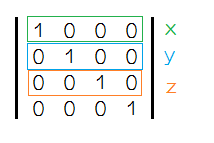
那么问题来了，最下面那行干啥用的？
一个顶点，坐标 (x,y,z)，这个是在笛卡尔坐标系中的表示，在 3D 世界中我们会将其转换为齐次坐标系，也就是变成了 (x,y,z,w)，这样的形式 (之前那么多图中 w=1)
矩阵的最后一行也就代表着齐次坐标，那么齐次坐标有啥作用？很多书上都会说齐次坐标可以区分一个坐标是点还是向量，点的话齐次项是 1，向量的话齐次项是 0(所以之前图中 w=1)
对于 webgl 中的 Matrix 来说齐次项有什么用处呢？或者说这个第四行改变了有什么好处呢？一句话概括 (敲黑板，划重点)
它可以让物体有透视的效果
举个例子，大名鼎鼎的透视矩阵，如图

在第四行的第三列就有值，而不像之前的是 0；还有一个细节就是第四行的第四列是 0，而不是之前的 1

写到这里的时候我纠结了，要不要详细的把正视和透视投影矩阵推导写一下，但是考虑到篇幅，实在是不好放在这里了，否则这篇文章要太长了，因为后面还有内容
大部分 3D 程序开发者可能不是很关注透视矩阵 (PMatrix)，只是知道有这一回事，用上这个矩阵可以近大远小，然后代码上也就是 glMatrix.setPerspective(……) 一下就行了
所以决定后面单独再写一篇，专门说下正视透视矩阵的推导、矩阵的优化这些知识
这里就暂且打住，我们先只考虑红框部分的矩阵所带来的变化

3/ webgl 的坐标系
我们前面 bb 了那么多，可以总结一下就是“ 矩阵是用来改变顶点坐标位置的！”，可以这么理解对吧 (不理解的再回去看下第二节里面的各种图)
那再看下文章开头说的 PMatrix／VMatrix／MMatrix 三个，这三个货都是矩阵啊，都是来改变顶点位置坐标的，再加上矩阵也是可以结合的啊，为什么这三个货要分开呢？
首先，这三个货分开说是为了方便理解，因为它们各司其职
MMatrix －－－> 模型矩阵（用于物体在世界中变化）
VMatrix －－－> 视图矩阵（用于世界中摄像机的变化）
PMatrix －－－> 透视矩阵
模型矩阵和视图矩阵具体的原理和关系我之前那篇射击小游戏文章里有说过，它们的改变的一般就是仿射变换，也就是平移、旋转之类的变化
这里稍微回忆一下原理，具体细节就不再说了
这两货一个是先旋转，后平移 (MMatrix)，另一个是先平移，后旋转 (VMatrix)
但就这个小区别，让人感觉一个是物体本身在变化，一个是摄像机在变化

好啦，重点说下 PMatrix。这里不是来推导出它如何有透视效果的，这里是讲它除了透视的另一大隐藏的功能
说到这里，先打一个断点，然后我们思考另一个问题

canvas2D 中和 webgl 中画布的区别
它们在 DOM 中的宽高都是通过设置 canvas 标签上 width 和 height 属性来设置的，这很一致。但 webgl 中我们的坐标空间是-1 ~ 1

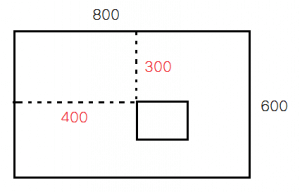
(width=800,height=600 中 canvas2D 中，矩形左顶点居中时，rect 方法的前两个参数)

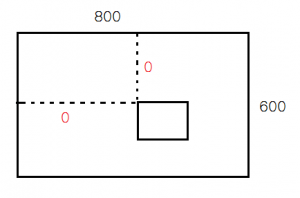
(width=800,height=600 中 webgl 中，矩形左顶点居中时，左顶点的坐标)

我们会发现 x 坐标小于-1 或者大于 1 的的话就不会展示了 (y 同理)，x 和 y 很好理解，因为屏幕是 2D 的，画布是 2D 的，2D 就只有 x，y，也就是我们直观上所看到的东西
那 z 坐标靠什么来看到呢？

对比

首先至少有两个物体，它们的 z 坐标不同，这个 z 坐标会决定它们在屏幕上显示的位置（或者说覆盖）的情景，让我们试试看

var aPo = [

-0.2, -0.2, -0.5,

0.2, -0.2, -0.5,

0.2, 0.2, -0.5,

-0.2, 0.2, -0.5

];

var aIndex = [0, 1, 2, 0, 2, 3];

webgl.bindBuffer(webgl.ARRAY_BUFFER, webgl.createBuffer());

webgl.bufferData(webgl.ARRAY_BUFFER, new Float32Array(aPo), webgl.STATIC_DRAW);

webgl.vertexAttribPointer(aPosition, 3, webgl.FLOAT, false, 0, 0);

webgl.vertexAttrib3f(aColor, 1, 0, 0);

webgl.bindBuffer(webgl.ELEMENT_ARRAY_BUFFER, webgl.createBuffer());

webgl.bufferData(webgl.ELEMENT_ARRAY_BUFFER, new Uint16Array(aIndex), webgl.STATIC_DRAW);

// 先画一个z轴是-0.5的矩形，颜色是红色

webgl.drawElements(webgl.TRIANGLES, 6, webgl.UNSIGNED_SHORT, 0);

aPo = [

0, -0.4, -0.8,

0.4, -0.4, -0.8,

0.4, 0, -0.8,

0, 0, -0.8

];

webgl.bindBuffer(webgl.ARRAY_BUFFER, webgl.createBuffer());

webgl.bufferData(webgl.ARRAY_BUFFER, new Float32Array(aPo), webgl.STATIC_DRAW);

webgl.vertexAttribPointer(aPosition, 3, webgl.FLOAT, false, 0, 0);

webgl.vertexAttrib3f(aColor, 0, 1, 0);

// 再画一个z轴是-0.8的矩形，颜色是绿色

webgl.drawElements(webgl.TRIANGLES, 6, webgl.UNSIGNED_SHORT, 0);

注意开启深度测试，否则就没戏啦
（不开启深度测试，计算机会无视顶点的 z 坐标信息，只关注 drawElements(drawArrays) 方法的调用顺序，最后画的一定是最上一层）

代码中 A 矩形 (红色) 的 z 值为-0.5, B 矩形 (绿色) 的 z 值为-0.8，最终画布上谁会覆盖谁呢？
如果我问的是 x＝0.5 和 x＝0.8 之间，谁在左，谁在右，我相信每个人都确定知道，因为这太熟了，屏幕就是 2D 的，画布坐标 x 轴就是右大左小就是这样的嘛

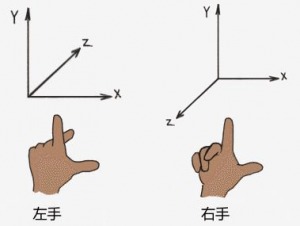
那我们更深层的考虑下为什么 x 和 y 的位置没人怀疑，因为“ 左手坐标系” 和“ 右手坐标系” 中 x，y 轴是一样的，如图所示

而左手坐标系和右手坐标系中的 z 轴正方向不同，一个是屏幕向内，一个是屏幕向外，所以可以认为
如果左手坐标系下，B 矩形 (z=-0.8) 小于 A 矩形 (z=-0.5)，那么理应覆盖了 A 矩形，右手坐标系的话恰恰相反

事实胜于雄辩，我们所以运行一下代码

查看结果：https://vorshen.github.io/3Dmaze/3.html

可以看到 B 矩形是覆盖了 A 矩形的，也就意味着 webgl 是左手坐标系

excuse me？？？所有文章说 webgl 都是右手坐标系啊，为什么这里居然是左手坐标系？

答案就是 webgl 中所说的右手坐标系，其实是一种规范，是希望开发者一起遵循的规范，但是 webgl 本身，是不在乎物体是左手坐标系还是右手坐标系的

可事实在眼前，webgl 左手坐标系的证据大家也看到了，这是为什么？刚刚说的有点笼统，不应该是“webgl 是左手坐标系”，而应该说“webgl 的裁剪空间是按照左手坐标系来的”

裁剪空间词如其名，就是用来把超过坐标空间的东西切割掉 (-1 ~ 1)，其中裁剪空间的 z 坐标就是按照左手坐标系来的

代码中我们有操作这个裁剪空间吗？有！回到断点的位置！

就是 PMatrix 它除了达成透视效果的另一个能力！
其实无论是 PMatrix(透视投影矩阵) 还是 OMatrix(正视投影矩阵)，它们都会操作裁剪空间，其中有一步就是将左手坐标系给转换为右手坐标系

怎么转化的，来，我们用这个单位矩阵试一下

1 0 0 0
0 1 0 0
0 0 -1 0
0 0 0 1

只需要我们将 z 轴反转，就可以得到将裁剪空间由左手坐标系转变为右手坐标系了。用之前的矩形 A 和矩形 B 再试一次看看

地址：https://vorshen.github.io/3Dmaze/4.html

果然如此！

这样我们就了解到了 webgl 世界中几个最为关键的 Matrix 了

4/ 结语
至于具体的 PMatrix 和 OMatrix 是怎么来的，Matrix 能否进行一些优化，我们下次再说~

有疑问和建议的欢迎留言一起讨论~

原创文章转载请注明：

转载自AlloyTeam：http://www.alloyteam.com/2017/01/getting-started-with-webgl-world-matrix/

分享到:

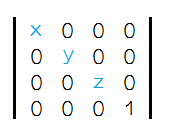
ervinewell 2017 年 9 月 8 日

线性代数都快忘完了 (:зゝ∠)

回复
刚刚好 2017 年 2 月 18 日

回复
Lcina 2017 年 1 月 18 日

沙发，看的我赶紧去恶补一下矩阵知识

回复

AlloyTeam

AlloyTeam

ervinewell 2017 年 9 月 8 日

刚刚好 2017 年 2 月 18 日

Lcina 2017 年 1 月 18 日

发表评论